Trabajo1

Por: Kevin Carrasco

Introducción

La investigación sobre percepción de desigualdad económica ha tenido un auge durante los últimos años (ver Mijs 2021; también Cruces, Perez-Truglia, and Tetaz 2013).

Específicamente, se ha encontrado evidencia sobre que… (Mijs 2021). De todas formas, Cruces, Perez-Truglia, and Tetaz (2013) plantea que…

Así mismo, Mijs señala que… (2021)

Aunque ambos concluyen que… (Mijs 2021; Cruces, Perez-Truglia, and Tetaz 2013)

Análisis

Una vez que tenemos recodificadas nuestras variables en el archivo de preparación y logramos exportar la base de datos procesada en la carpeta input/data, abrimos un documento de quarto (.qmd) para realizar el análisis.

Al trabajar con quarto (y al intentar renderizar), el documento leerá todos lo que esté escrito en el documento desde 0, por lo que es necesario siempre cargar de nuevo los paquetes y bases de datos.

Primero cargamos los paquetes:

pacman::p_load(dplyr, sjmisc, car, sjlabelled, stargazer, haven, sjPlot, ggplot2, psych, kableExtra, corrplot, texreg, summarytools)

y la base procesada

load("input/data/elsoc2016_proc.RData")

Análisis descriptivo

view(dfSummary(proc_data, headings=FALSE)) %>%    kable(.,"markdown")

Switching method to 'browser'

Output file written: C:\Users\kevin\AppData\Local\Temp\Rtmp0cBCsL\file207c3ba9351c.html

Switching method to 'browser'

Output file written: C:\Users\kevin\AppData\Local\Temp\Rtmp0cBCsL\file207c52b87a5d.html

x
C:0cBCsL207c52b87a5d.html

sjmisc::descr(proc_data,
      show = c("label","range", "mean", "sd", "NA.prc", "n"))%>% # Selecciona estadísticos
      kable(.,"markdown") # Esto es para que se vea bien en quarto

Table 1: Descriptivos

	var	label	n	NA.prc	mean	sd	range
1	ideal	Este barrio es ideal para mi	2926	0.0341647	2.615174	1.0202541	4 (0-4)
3	integracion	Me siento integrado en este barrio	2923	0.1366587	2.565515	0.9993502	4 (0-4)
2	identificacion	Me identifico con la gente de este barrio	2923	0.1366587	2.523777	0.9884856	4 (0-4)
7	pertenencia	Me siento parte de este barrio	2925	0.0683293	2.627692	0.9878809	4 (0-4)
4	m01	Nivel educacional	2925	0.0683293	5.260513	2.2015019	9 (1-10)
6	m0_sexo	Sexo del entrevistado	2927	0.0000000	1.602665	0.4894300	1 (1-2)
5	m0_edad	Edad del entrevistado	2927	0.0000000	46.090878	15.2867983	70 (18-88)

En la Table 1 podemos observar los descriptivos generales de la base de datos procesada.

Y si queremos visualizar algo más:

proc_data %>% select(ideal, integracion, identificacion, pertenencia) %>% 
  sjPlot::plot_stackfrq()+
  theme(legend.position = "bottom")

En la (plot-descriptivos?) podemos ver la distribución de las variables de cohesión barrial, donde se puede observar que más del 65% de la muestra está de acuerdo o totalmente de acuerdo con las afirmaciones indicadas.

Asociación de variables

Podemos ver la asociación de todas las variables, como lo muestra la ?@cor-complete

M <- cor(proc_data, use = "complete.obs") # Usar solo casos con observaciones completas

corrplot.mixed(M)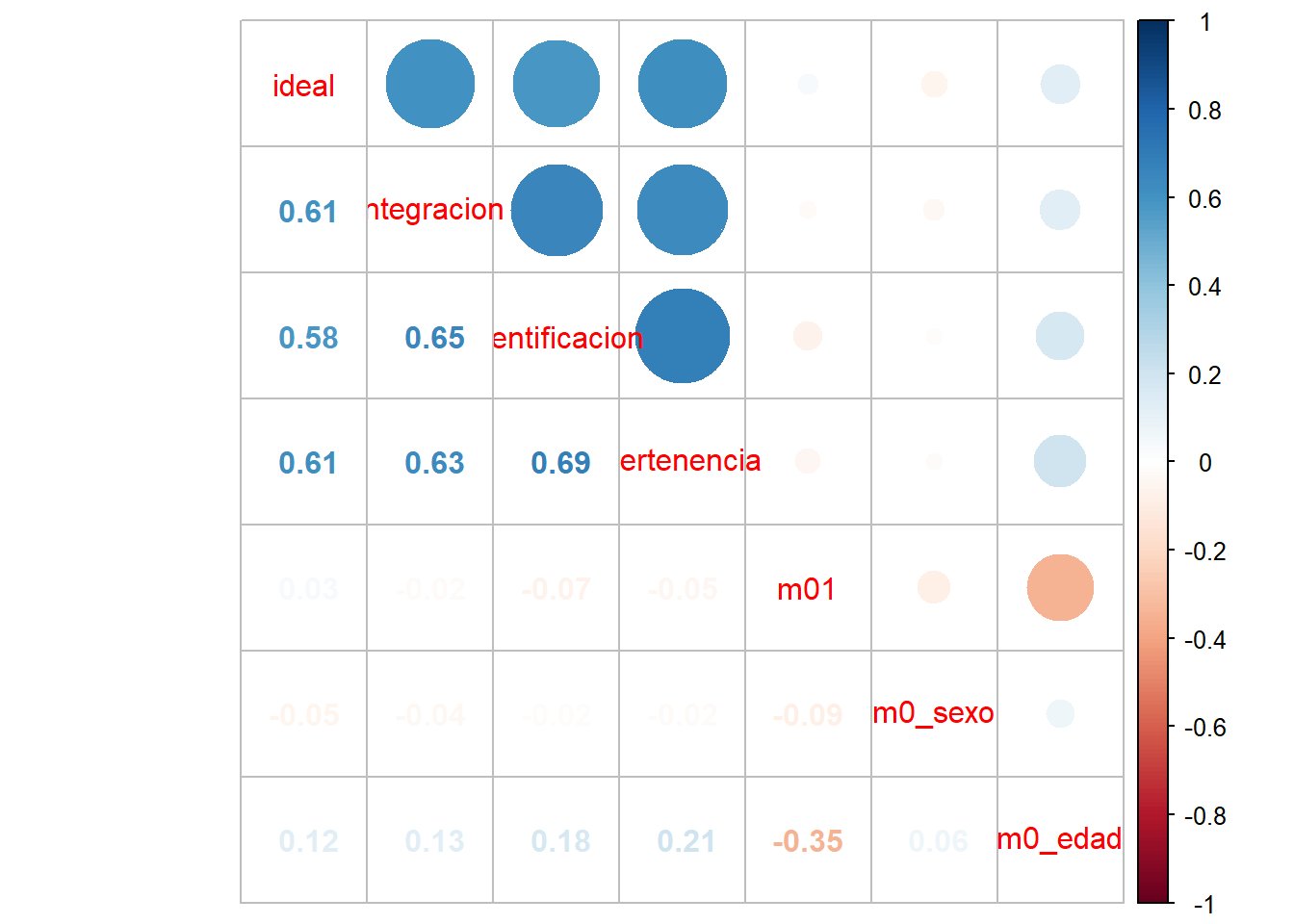

o podemos ver específicamente la asociación de las variables de cohesión barrial

M2 <- cor(dplyr::select(proc_data, ideal, integracion, identificacion, pertenencia), use = "complete.obs")
corrplot.mixed(M2)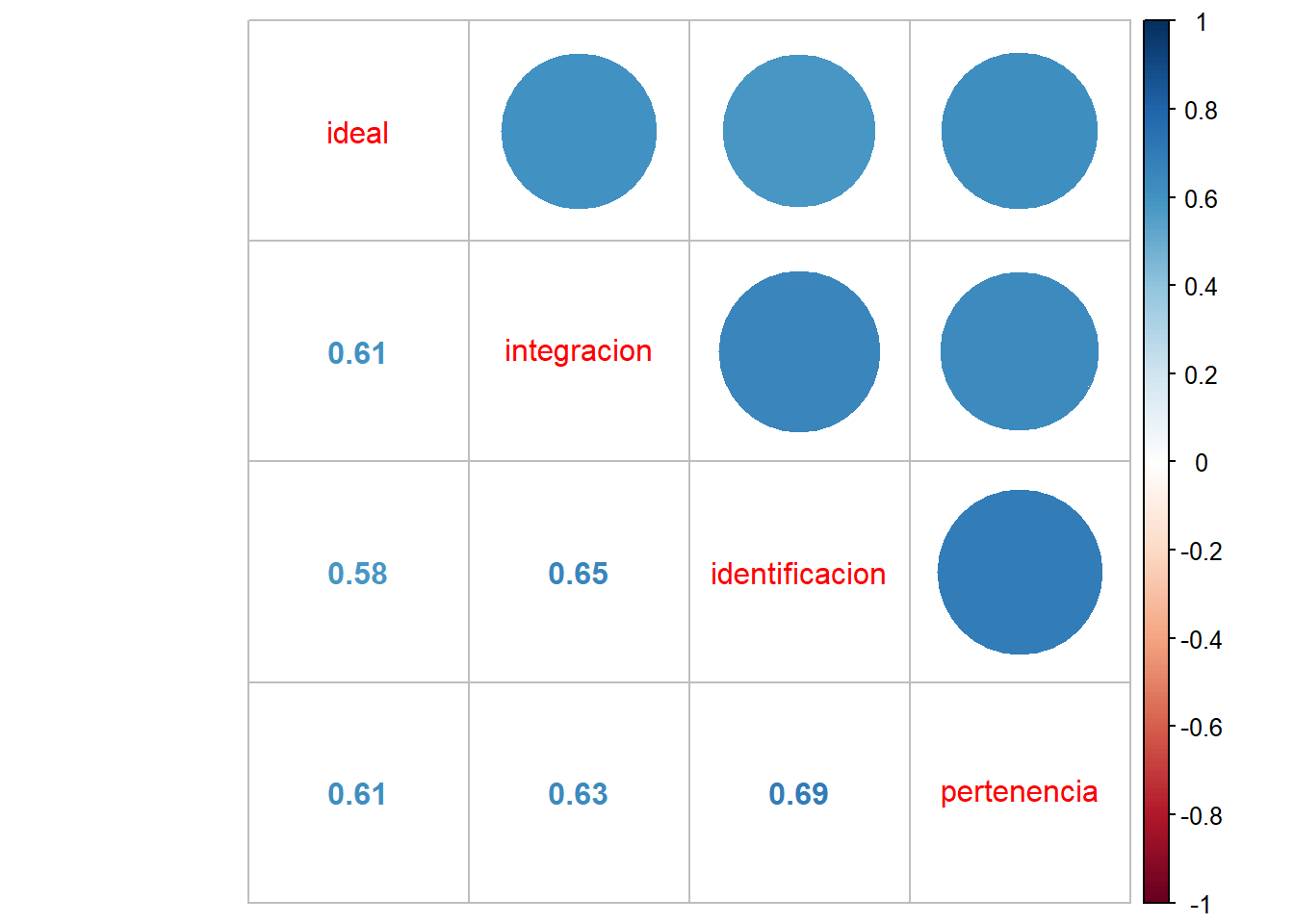

La ?@cor-cohesion muestra que la asociación de las cuatro variables de cohesión barrial es alta y positiva, según Cohen (1998). En general el tamaño de efecto varía entre 0.58 la más baja y 0.69 la más alta.

Construcción de escala

psych::alpha(dplyr::select(proc_data, ideal, integracion, identificacion, pertenencia))


Reliability analysis   
Call: psych::alpha(x = dplyr::select(proc_data, ideal, integracion, 
    identificacion, pertenencia))

  raw_alpha std.alpha G6(smc) average_r S/N    ase mean   sd median_r
      0.87      0.87    0.84      0.63 6.8 0.0039  2.6 0.85     0.62

    95% confidence boundaries 
         lower alpha upper
Feldt     0.86  0.87  0.88
Duhachek  0.86  0.87  0.88

 Reliability if an item is dropped:
               raw_alpha std.alpha G6(smc) average_r S/N alpha se   var.r med.r
ideal               0.85      0.85    0.80      0.66 5.8   0.0047 0.00086  0.65
integracion         0.84      0.84    0.78      0.63 5.1   0.0053 0.00299  0.61
identificacion      0.83      0.83    0.76      0.62 4.9   0.0055 0.00015  0.61
pertenencia         0.83      0.83    0.76      0.62 4.8   0.0055 0.00121  0.61

 Item statistics 
                  n raw.r std.r r.cor r.drop mean   sd
ideal          2926  0.83  0.83  0.73   0.69  2.6 1.02
integracion    2923  0.85  0.85  0.78   0.73  2.6 1.00
identificacion 2923  0.86  0.86  0.80   0.74  2.5 0.99
pertenencia    2925  0.86  0.86  0.80   0.75  2.6 0.99

Non missing response frequency for each item
                  0    1    2    3    4 miss
ideal          0.04 0.14 0.13 0.55 0.14    0
integracion    0.04 0.15 0.14 0.56 0.12    0
identificacion 0.04 0.15 0.16 0.55 0.10    0
pertenencia    0.03 0.14 0.12 0.57 0.13    0

La consistencia interna de una posible escala entre estos cuatro ítems es de 0.87, lo que representa una alta consistencia interna. Si quitaramos alguno de estos ítems la consistencia interna solo bajaría, así que podemos construir una escala con los cuatro ítems.

proc_data <- proc_data %>% 
  rowwise() %>% 
  mutate(cohesion_barrial = sum(ideal, integracion, identificacion, pertenencia))
summary(proc_data$cohesion_barrial)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
   0.00    8.00   12.00   10.33   12.00   16.00      10

y la podemos visualizar en un gráfico:

ggplot(proc_data, aes(x = cohesion_barrial)) +
  geom_histogram(binwidth=0.6, colour="black", fill="yellow") +
  theme_bw() +
  xlab("Cohesión barrial") +
  ylab("Cantidad")

Warning: Removed 10 rows containing non-finite values (`stat_bin()`).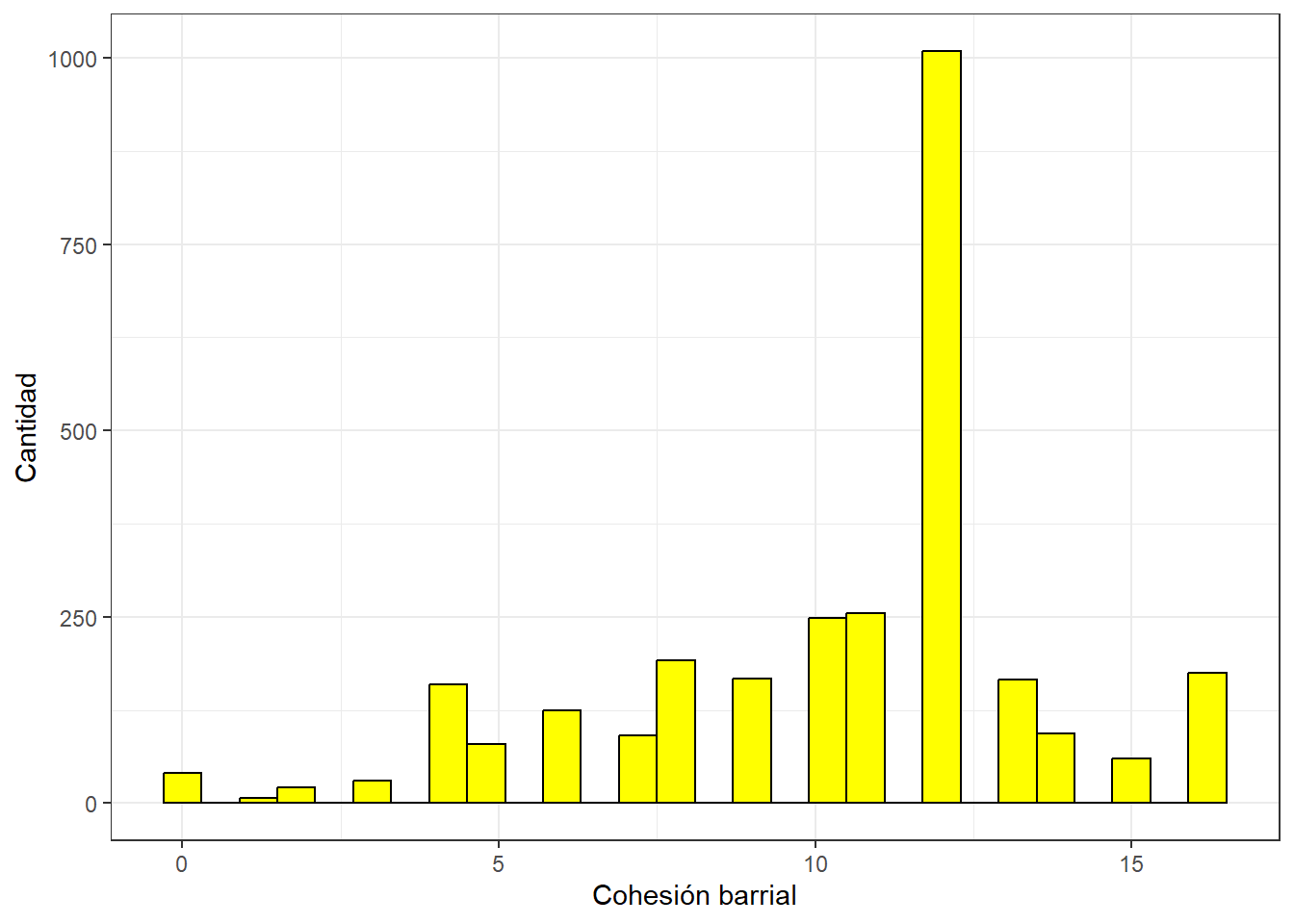

El (plot-cohesion?) muestra la distribución de la nueva escala de Cohesión Barrial que construimos. En general, la mayor concentración de casos está en la categoría 12 y que sumado a un promedio de 10.33 según los descriptivos anteriores, podríamos afirmar que la cohesión barrial en Chile es alta.

Regresiones

reg5 <- lm(cohesion_barrial ~ m0_edad, data=proc_data)
reg6 <- lm(cohesion_barrial ~ m0_edad + m01, data=proc_data)
reg7 <- lm(cohesion_barrial ~ m0_edad + m01 + m0_sexo, data=proc_data)

knitreg(list(reg5, reg6, reg7), 
        custom.model.names = c("Modelo 1",
                               "Modelo 2",
                               "Modelo 3"),
        custom.note = "*** p < 0.001; ** p < 0.01; * p < 0.05",
        custom.coef.names = c("Intercepto", 
                              "Edad",
                              "Educación", 
                              "Mujer <br> <i>(Ref. Hombre)</i>"),
        caption = "Cohesión barrial",
        caption.above = TRUE)

Cohesión barrial
	Modelo 1	Modelo 2	Modelo 3
Intercepto	8.42^***	7.96^***	8.50^***
	(0.20)	(0.30)	(0.36)
Edad	0.04^***	0.04^***	0.04^***
	(0.00)	(0.00)	(0.00)
Educación		0.06^*	0.06
		(0.03)	(0.03)
Mujer (Ref. Hombre)			-0.33^**
			(0.13)
R²	0.03	0.04	0.04
Adj. R²	0.03	0.04	0.04
Num. obs.	2917	2915	2915
* p < 0.001; p < 0.01; * p < 0.05

ggeffects::ggpredict(reg7, terms = c("m0_sexo")) %>%
  ggplot(aes(x=x, y=predicted)) +
  geom_bar(stat="identity", color="grey", fill="grey")+
  geom_errorbar(aes(ymin = conf.low, ymax = conf.high), width=.1) +
  labs(title="Sexo", x = "", y = "") +
  theme_bw() +
  scale_x_continuous(name = "",
                     breaks = c(0,1),
                     labels = c("Hombre", "Mujer"))+
  scale_y_continuous(limits = c(0,16), 
                     breaks = seq(0,16, by = 1))

References

Cruces, Guillermo, Ricardo Perez-Truglia, and Martin Tetaz. 2013. “Biased Perceptions of Income Distribution and Preferences for Redistribution: Evidence from a Survey Experiment.” Journal of Public Economics 98 (February): 100–112. https://doi.org/10.1016/j.jpubeco.2012.10.009.

Mijs, Jonathan J B. 2021. “The Paradox of Inequality: Income Inequality and Belief in Meritocracy Go Hand in Hand.” Socio-Economic Review 19 (1): 7–35. https://doi.org/10.1093/ser/mwy051.